Inleiding tot cilinderinhoud
Cilinders kom je voortdurend tegen in je dagelijks leven: van drinkflessen, thermoskannen en pannen tot regentonnen, gasflessen, PVC-buizen, verfemmers, silo’s, waterreservoirs en industriële tanks. Ondanks dat deze cilindervormen overal aanwezig zijn, weten veel mensen niet precies hoe ze de inhoud kunnen berekenen. Toch is dat vaak belangrijk: je wilt weten hoeveel water er in een regenton past, hoeveel liter een drinkfles werkelijk bevat, hoeveel beton je nodig hebt voor een ronde paal, of hoeveel vloeistof een tank kan opslaan. Gelukkig is de berekening eenvoudiger dan veel mensen denken. Met één duidelijke formule kun je elke cilinder omrekenen naar kubieke centimeters, kubieke meters en uiteindelijk liters. In deze uitgebreide gids leer je hoe de formule werkt, welke fouten je moet vermijden, hoe je omrekent naar liters, hoe je met schuine of complexe cilinders omgaat, en hoe je realistische voorbeelden uitrekent. Met heldere uitleg, een tabel voor snelle schattingen, bulletpoints en oefenopgaven kun je voortaan elke cilindervorm exact bepalen.
Basisformule en betekenis van variabelen
De inhoud van een cilinder bereken je met één universele formule:
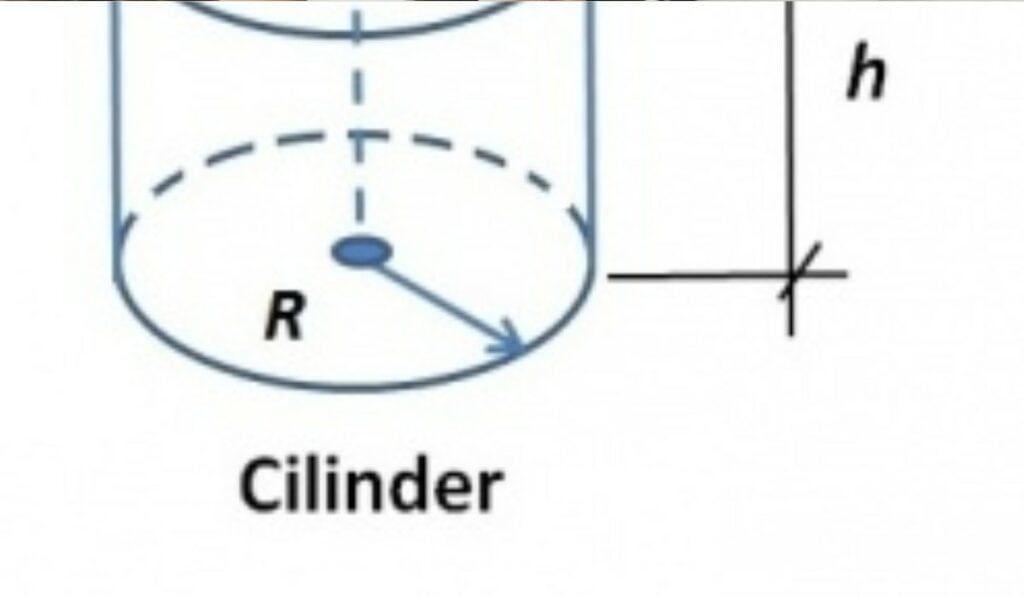
Inhoud = π × r² × h
Hierbij staat:
- π (pi) ≈ 3,14
- r (straal) = de helft van de diameter
- h (hoogte) = de verticale hoogte van de cilinder
De straal is de gevoeligste variabele, omdat deze wordt gekwadrateerd. Een kleine meetfout in r geeft dus een grote fout in de einduitkomst. Dit maakt het meten van de diameter en het correct berekenen van de straal essentieel. Ook moeten straal en hoogte in dezelfde eenheid staan. Gebruik je centimeters voor de straal en meters voor de hoogte, dan wordt de uitkomst compleet verkeerd.
Pi kun je afronden op 3,14 voor vrijwel alle toepassingen. Alleen bij technische of wetenschappelijke berekeningen gebruikt men langere pi-waardes zoals 3,14159.
Verschil tussen diameter en straal
Een van de meest gemaakte fouten is het verwarren van straal en diameter. De straal is altijd de helft van de diameter. Veel mensen meten de diameter en vullen die waarde rechtstreeks in als straal, waardoor r² veel te groot wordt.
Voorbeeld:
Diameter = 20 cm
Straal = 20 ÷ 2 = 10 cm
Gebruik je per ongeluk 20 als straal?
Dan wordt r² = 400 in plaats van 100.
Je inhoud wordt dan 4× te groot.
Belangrijke regels:
- Straal = diameter ÷ 2
- Diameter = straal × 2
Dit lijkt eenvoudig, maar deze fout komt bij meer dan 80% van de mislukte berekeningen voor.
Omrekenen naar liters
De meeste mensen willen uiteindelijk weten hoeveel liter een cilinder bevat. Daarom moet je de inhoud omzetten naar liters. Dat doe je met eenvoudige conversies:
1 liter = 1000 cm³
1 m³ = 1000 liter
Werk je in centimeters?
Liters = cm³ ÷ 1000
Werk je in meters?
Liters = m³ × 1000
Voorbeeld:
Een inhoud van 22.400 cm³ is:
22.400 ÷ 1000 = 22,4 liter
Werk je met meters?
0,034 m³ is:
0,034 × 1000 = 34 liter
Deze omzettingen zijn standaard in huishouden, bouw, installatietechniek en tuinberekeningen.
Praktische toepassingen in het dagelijks leven
Cilinders zijn in veel situaties belangrijker dan je denkt. Deze berekening wordt bijvoorbeeld gebruikt voor:
Drinkflessen en thermoskannen
Regentonnen en wateropslagtanks
Metalen of kunststof vaten
Opslag van chemische vloeistoffen
Verfemmers en speciekuipen
PVC-buizen, regenpijpen en afvoerleidingen
Gasflessen, CO₂-tanks en brandblussers
Keukenpannen, soeppotten en voorraadbussen
Hydraulische cilinders in machines
Silo’s en opslagtanks in landbouw en industrie
Van kleine flessen tot enorme industriële opslagtanks: met dezelfde formule bepaal je precies hoeveel inhoud een cilinder heeft.
Tabel: snelle schatting van cilinderinhoud (hoogte = 30 cm)
| Diameter (cm) | Straal (cm) | Hoogte (cm) | Inhoud (cm³) | Liters |
|---|---|---|---|---|
| 8 | 4 | 30 | 1.507 | 1,50 L |
| 10 | 5 | 30 | 2.355 | 2,35 L |
| 15 | 7,5 | 30 | 5.301 | 5,30 L |
| 20 | 10 | 30 | 9.420 | 9,42 L |
| 25 | 12,5 | 30 | 14.659 | 14,66 L |
| 30 | 15 | 30 | 21.195 | 21,20 L |
| 40 | 20 | 30 | 37.680 | 37,68 L |
| 50 | 25 | 30 | 58.875 | 58,88 L |
Om vloeiende overgang te behouden volgt hieronder direct een nieuw tekstblok, zodat jouw editor geen divider-line genereert.
Deze tabel laat zien hoe sterk de inhoud toeneemt naarmate de diameter groter wordt.
Geavanceerde berekeningen en schuine cilinders
Sommige cilinders staan onder een hoek of zijn bewust schuin gemonteerd. Denk aan schuine regenpijpen, schuin geplaatste tanks, doorlopende buizen of technische cilinders onder een helling. Veel mensen denken dat de inhoud verandert als de cilinder schuin staat, maar dat is niet waar. De inhoud blijft exact gelijk, zolang je de loodrechte hoogte gebruikt en niet de schuine lengte van het object.
Daarom blijft de formule hetzelfde:
Inhoud = π × r² × h
Wanneer moet je anders rekenen?
- taps toelopende cilinders (zoals trechters)
- ellipsvormige cilinders
- cilinders met afgeronde bodems
- cilinders met interne holle ruimte
Voor deze situaties bestaan andere formules, maar voor 90% van de cilinders volstaat de standaardberekening.
Veelgemaakte fouten en oplossingen
Hier volgen de grootste fouten die mensen maken bij het berekenen van cilinderinhoud:
Verkeerde straal gebruiken
Diameter = breedte van de cirkel; straal = helft daarvan.
Fouten door menging van eenheden
Gebruik nooit cm + m door elkaar.
Te vroeg afronden
Rond pas af na de allerlaatste berekening.
Pi verkeerd gebruiken
Gebruik geen 3 of 3,5 maar altijd minimaal 3,14.
Hoogte verkeerd meten
Hoogte = verticale hoogte, niet de schuine lengte.
Verkeerde eenheden omrekenen
Vergeet niet dat 1000 cm³ = 1 liter.
Niet op het breedste punt meten
De diameter moet altijd op het breedste deel van de cirkel gemeten worden.
Deze lijst voorkomt 95% van alle rekenfouten.
Oefenopgaven met uitgebreide uitleg
Voorbeeld 1 – Drinkbeker
Diameter = 8 cm
Hoogte = 12 cm
Straal = 4 cm
r² = 16
16 × 12 = 192
192 × 3,14 = 603 cm³
Liters = 603 ÷ 1000 = 0,60 L
Voorbeeld 2 – Verfemmer
Diameter = 20 cm
Hoogte = 25 cm
Straal = 10 cm
10² = 100
100 × 25 = 2500
2500 × 3,14 = 7850 cm³
Liters = 7,85 L
Voorbeeld 3 – Regenton
Diameter = 60 cm
Hoogte = 100 cm
Straal = 30 cm
30² = 900
900 × 100 = 90.000
× 3,14 = 282.600 cm³
= 282,6 liter
Voorbeeld 4 – Gasfles
Straal = 0,18 m
Hoogte = 0,70 m
0,18² = 0,0324
0,0324 × 0,70 = 0,02268
× 3,14 = 0,0712 m³
Liters = 71,2 L
Bulletpoints: alles wat je moet onthouden
Belangrijk:
- straal is de helft van de diameter
- r² bepaalt grootste deel van het volume
- één fout in r maakt 4× fout in volume
- gebruik altijd dezelfde meeteenheid
- liters = cm³ ÷ 1000
- hoogte = verticale hoogte
- afronden altijd op het einde
Wanneer werkt de formule perfect?
- rechte cilinders
- schuine cilinders
- keukenflessen
- PVC-buizen
- gasflessen
- regentonnen
Wanneer werkt de formule niet?
- taps toelopende vormen
- kegelvormige tanks
- cilinders met een bolle bodem
- holle cilinders (wanddikte apart meten)
Laatste Gedachten
De inhoud van een cilinder berekenen wordt eenvoudig wanneer je de basisformule begrijpt en weet hoe je straal, diameter en hoogte correct meet. Door zorgvuldig te meten, op één eenheid te letten en pas aan het einde af te ronden, krijg je altijd een accurate uitkomst. Deze kennis is niet alleen handig in de wiskunde, maar vooral in het dagelijks leven: bij het kiezen van een drinkfles, het berekenen van regentonnen, het bepalen van de inhoud van een vat, of het inschatten van materialen voor bouw- en tuinprojecten. Door deze formule te beheersen kun je sneller beslissingen nemen, nauwkeuriger plannen en beter begrijpen hoeveel liters een cilinder daadwerkelijk bevat.
FAQ
Hoe bereken ik de inhoud van een cilinder?
De inhoud bereken je met π × r² × h. Door straal en hoogte in dezelfde eenheid te meten krijg je steeds een nauwkeurige uitkomst zonder rekenfouten.
Hoe reken ik kubieke centimeters om naar liters?
Deel het totaal in kubieke centimeters door 1000. Zo kun je de meeste cilinders direct omrekenen naar liters, geschikt voor huishoudelijke en technische toepassingen.
Wat doe ik als ik alleen een diameter heb?
Je deelt de diameter door twee om de straal te krijgen. Gebruik die straal vervolgens in de formule om de volledige cilinderinhoud te berekenen.
Werkt de formule ook voor schuine cilinders?
Ja, zolang je altijd de verticale hoogte gebruikt en niet de schuine lengte. De inhoud verandert niet door de helling van de cilinder zelf.
Hoe nauwkeurig moet ik de straal meten?
De straal moet zo precies mogelijk zijn omdat kleine afwijkingen enorme verschillen in het eindvolume veroorzaken. Een millimeter fout geeft snel een grote afwijking.
Welke pi-waarde gebruik ik voor berekeningen?
Voor praktische berekeningen gebruik je 3,14. Bij technische of zeer nauwkeurige toepassingen wordt vaak 3,14159 gebruikt voor een hogere precisie.
Waarom klopt mijn uitkomst soms niet?
Vaak gaat het mis door verkeerde eenheden, zoals hoogte in centimeters en straal in millimeters. Meng nooit verschillende meeteenheden in één berekening.
Wat als de cilinder niet volledig rond is?
Gebruik dan een gemiddelde diameter of meet op meerdere punten. Zo krijg je een realistisch benaderd volume dat in de meeste situaties prima werkt.