Het berekenen van de inhoud van een cilinder is een essentiële vaardigheid in wiskunde, techniek en dagelijks gebruik. Of je nu vloeistoffen in liters wilt meten, materialen wilt inschatten of het volume van objecten wilt berekenen, met de juiste formule en methode is dit eenvoudig en nauwkeurig uit te voeren. In dit uitgebreide artikel bespreken we wat een cilinder is, hoe de inhoud wordt berekend, diverse voorbeelden, omzetting naar liters, veelgemaakte fouten, vergelijkingen met andere vormen, praktische toepassingen, rekenoefeningen, en scenario’s uit het dagelijks leven.
Wat is een cilinder?
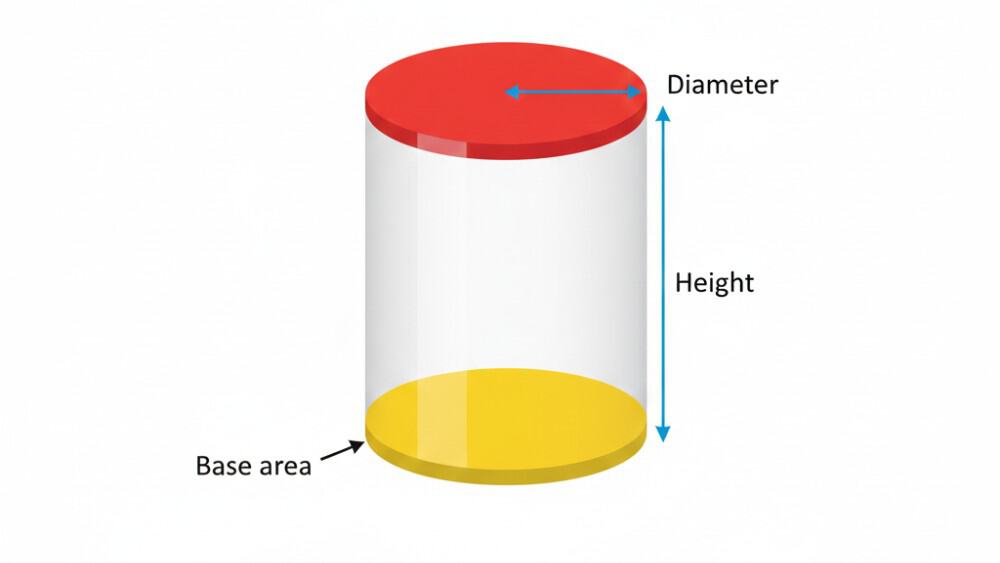
Een cilinder is een driedimensionale figuur met twee identieke cirkelvormige bases die parallel liggen en verbonden worden door een gebogen oppervlak. Net zoals je bij wiskundige berekeningen soms een gemiddelde cijfer berekenen moet, helpt het begrijpen van de eigenschappen van een cilinder bij het oplossen van meetkundige vraagstukken.
- Kenmerken: Twee gelijke cirkels, rechte hoogte en ronde zijkant.
- Voorbeelden uit het dagelijks leven: Drinkblikjes, waterflessen, pijpen, kaarsen, zuilen.
- Eigenschappen: Symmetrisch, constante doorsnede langs de hoogte, makkelijk te meten.
- Praktisch gebruik: Wordt veel gebruikt bij opslag van vloeistoffen, constructies, en technische ontwerpen.
Door de eigenschappen goed te begrijpen, kun je de juiste formule voor het volume van een cilinder toepassen en nauwkeurige resultaten verkrijgen.
De formule voor volume van een cilinder
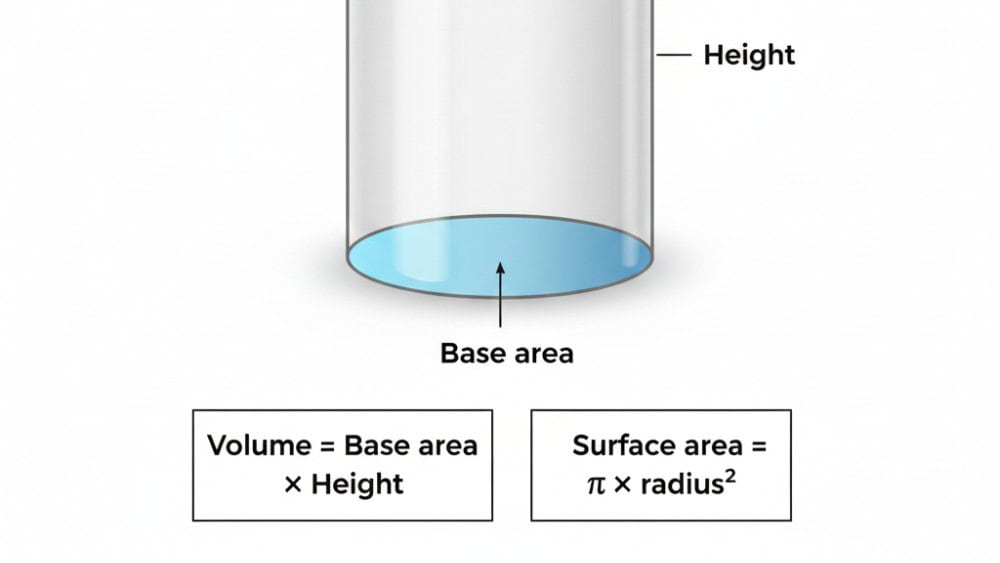
De inhoud van een cilinder wordt berekend met de bekende formule: V = π × r² × h
- V = volume van de cilinder
- r = straal van de cirkelvormige basis
- h = hoogte van de cilinder
- π (pi) ≈ 3,14159
- Let op: Zorg dat de straal en hoogte in dezelfde eenheid staan.
- Toepassing: Van wateropslag tot bouwkundige berekeningen, zoals pijpen, kolommen en tanks.
Met deze formule kun je direct het volume van elke cilinder berekenen, ongeacht de grootte, en het resultaat in kubieke meters of liters omrekenen. Hier vind je de formules inhoud cilinder berekenen die je stap voor stap kunt toepassen.
Stap-voor-stap rekenvoorbeelden
Het is makkelijker te begrijpen met concrete voorbeelden.
- Voorbeeld 1: Een drinkblik met straal 3 cm en hoogte 12 cm. Bereken het volume: V = π × 3² × 12 ≈ 339,29 cm³.
- Voorbeeld 2: Een watertank met straal 1 m en hoogte 2 m: V = π × 1² × 2 ≈ 6,28 m³.
- Voorbeeld 3: Bereken het volume van een kaarsvormige cilinder met straal 5 cm en hoogte 20 cm: V = π × 25 × 20 ≈ 1570 cm³.
- Tips:
- Rond pas af aan het einde van de berekening voor maximale precisie.
- Noteer duidelijk alle stappen voor controle.
- Controleer of straal en hoogte in dezelfde eenheid staan.
Door stap-voor-stap te rekenen, verklein je de kans op fouten en krijg je altijd een nauwkeurig resultaat.
- Rond pas af aan het einde van de berekening voor maximale precisie.
Inhoud omrekenen naar liters
Vaak wil je het volume in liters weten in plaats van kubieke centimeters of meters.
- Formule: 1 liter = 1 dm³ = 1000 cm³
- Voorbeeld: Een cilinder van 5000 cm³ bevat 5 liter.
- Praktische tip: Controleer altijd of je de juiste eenheid gebruikt bij berekeningen.
- Gebruik: Handig voor vloeistoffen zoals water, olie of chemicaliën in cilindercontainers.
- Extra tip: Voor huishoudelijke toepassingen zoals een waterkoker of regenwatertank kun je zo het exacte volume inschatten.
Door de inhoud om te rekenen, kun je eenvoudig meten hoeveel vloeistof er in een cilinder past en dit direct praktisch toepassen in het dagelijks leven.
Veelgemaakte fouten bij cilinderberekening
Bij het berekenen van de inhoud van een cilinder maken mensen vaak dezelfde fouten:
- Verkeerde eenheden: Straal in cm en hoogte in m zonder omrekening leidt tot verkeerde resultaten.
- Pi vergeten: Veel beginners vergeten π of gebruiken een afgeronde waarde te vroeg.
- Kwadrateren van straal: Het kwadraat van de straal vergeten geeft een veel te klein volume.
- Hoogte verkeerd gemeten: Meet altijd loodrecht van de basis tot de bovenkant.
- Afrondingsfouten: Rond pas af aan het einde van de berekening.
Door deze fouten te vermijden, krijg je altijd een correct resultaat en kun je betrouwbare berekeningen uitvoeren voor studie en praktische toepassingen.
Vergelijking met andere vormen
Het is handig om cilinders te vergelijken met andere geometrische vormen om inzicht te krijgen in volumes:
- Rechthoekige doos: V = lengte × breedte × hoogte; cilinder is vaak compacter voor hetzelfde volume.
- Bol: V = 4/3 × π × r³; cilinders bevatten vaak meer volume bij dezelfde hoogte.
- Kegel: V = 1/3 × π × r² × h; een cilinder van dezelfde straal en hoogte bevat drie keer het volume van een kegel.
- Praktische tip: Kies de juiste vorm bij de opslag van vloeistoffen of bij het ontwerpen van objecten voor ruimtebesparing, net zoals je bij romeinse cijfers de juiste notatie kiest voor duidelijkheid en structuur.
Door vergelijkingen te maken, begrijp je beter hoe volume werkt en kun je praktische keuzes maken.
Toepassingen in het dagelijks leven
Cilinders kom je overal tegen, vaak zonder dat je het doorhebt:
- Keuken: Drinkblikken, olieflessen, maatbekers.
- Techniek: Watertanks, pijpleidingen, hydraulische cilinders.
- Bouw: Palen, kolommen en steunstructuren zijn vaak cilindervormig.
- Wetenschap: Proefbuisjes en laboratoriumapparatuur gebruiken cilinderberekeningen.
- Huishouden: Regenwatertonnen, opslagvaten, kaarsen en lampen.
Door de formule te kennen, kun je overal het volume snel bepalen, handig voor zowel praktische als academische toepassingen.
Extra oefeningen voor studenten
Het regelmatig oefenen helpt bij begrip en nauwkeurigheid.
- Oefening 1: Bereken het volume van een cilinder met straal 7 cm en hoogte 15 cm.
- Oefening 2: Een regenwatertank van 1,2 m straal en 2,5 m hoogte. Bereken het volume in liters.
- Oefening 3: Vergelijk een cilinder met een kegel van dezelfde straal en hoogte; hoeveel keer past de inhoud van de kegel in de cilinder?
- Tip: Noteer altijd alle stappen en controleer de eenheden.
Door oefeningen te maken, ontwikkel je een praktisch inzicht en leer je fouten voorkomen.
Scenario’s uit het dagelijks leven
- Scenario 1: Je wilt weten hoeveel water je regenton kan bevatten. Meet de straal en hoogte, bereken de inhoud en zet om naar liters.
- Scenario 2: Je ontwerpt een nieuwe zuil voor een tuinproject. Gebruik de formule om te controleren hoeveel materiaal nodig is.
- Scenario 3: In een laboratorium moet je een oplossing in een cilinderfles meten. Door het volume exact te berekenen voorkom je verspilling.
- Tip: Gebruik altijd dezelfde eenheid voor hoogte en straal en rond pas af aan het einde.
Door praktische scenario’s te oefenen, zie je direct het nut van cilinderberekeningen.
Laatste Gedachten: cilinder inhoud berekenen praktisch en inzichtelijk voor iedereen
Het correct berekenen van de cilinderinhoud is belangrijk voor school, studie en dagelijks gebruik. Met de formule, stap-voor-stapvoorbeelden, vergelijkingen, oefeningen en scenario’s uit het dagelijks leven vergroot je je vaardigheid. Door om te rekenen naar liters worden de berekeningen direct toepasbaar voor vloeistoffen, opslag en technische projecten, net zoals bij het omrekenen van fahrenheit naar celsius. Regelmatig oefenen met diverse voorbeelden vergroot de nauwkeurigheid en zekerheid bij berekeningen.
FAQ
Hoe bereken ik de inhoud van een cilinder?
Gebruik de formule V = π × r² × h. Meet straal en hoogte in dezelfde eenheid en vul in om het volume te berekenen. Rond pas af aan het einde voor precisie.
Kan ik de inhoud direct in liters berekenen?
Ja, eerst het volume in cm³ of m³ berekenen en daarna omrekenen: 1 liter = 1000 cm³. Zo krijg je een praktisch resultaat voor vloeistoffen.
Wat als ik de diameter weet in plaats van de straal?
De straal is de helft van de diameter. Deel de diameter door twee en gebruik r² in de formule voor het volume.
Welke fouten maken mensen vaak bij cilinderberekening?
Veelgemaakte fouten zijn verkeerde eenheden, π vergeten, straal niet kwadrateren, hoogte verkeerd meten en te vroeg afronden. Let hier goed op voor nauwkeurige resultaten.
Kan ik dit ook voor andere cilinderobjecten gebruiken?
Ja, de formule werkt voor alle cilinders zoals blikjes, pijpen, tanks en kaarsen, zolang de basis cirkelvormig is en de hoogte loodrecht gemeten wordt.